Hi, I’m Rado A. Rakotonarivo. My current position is Attaché Temporaire d’Enseignement et de Recherche at Ufr Informatique where I am giving computer science courses to bachelor and master students. Besides I work as a researcher at IRIF in the combinatorics team. In this page you will find useful information about me and what I am doing. You can also find my resume here (I hope it is up to date).
Research overview
My PhD thesis, entitled On the combinatorics of lattice polytopes : random sampling and enumeration, gathers several works on the lattice polytopes of $R^d$. My PhD advisors was Lionel Pournin and Julien David.
I mainly work on the lattice polytopes of $R^d$. In particular, it focuses on the combinatorics of the family of the d-dimensional lattice polytopes contained in the $[0,k]^d$ hypercube. Due to their elusive combinatorics, a direct approach using the symbolic method is out of reach. Hence, we made an original approach based on the description of a graph whose vertex set is the set of $(d,k)$-polytopes. In this graph, there is an edge between two polytopes if we can transform each of them into the other by an elementary move. These elementary moves are local operations performed on the polytopes. The connectedness of this graph made us study an uniform random sampler based on a Markov Chain for the $(d,k)$-polytopes of arbitrary dimension and also permited to obtain exhaustive enumeration algorithms. These are the main results gathered in my PhD thesis.
Recent works
- Computational methods for the enumeration of $(d,k)$-polytopes
Study of two enumeration algorithms for lattice polytopes contained in the $[0,k]^d$ hypercube: the first for the case where the lattice polytope is contained in the unit hypercube; the second for the case where k is greater than 1.
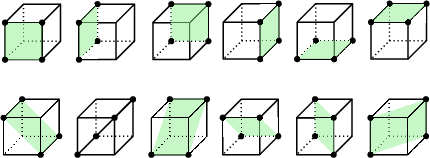
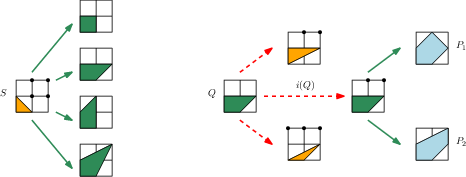
- Counting non-full dimensional polytopes with d+1 vertices in the unit cube.
- Enumerating lattice polygons contained in the 2 x 2 square obtained from the triangle S.